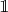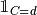Factor algebra¶
In the section Probabilistic models in symfer, we have seen that a model consists of factors: arrays of (usually) probabilities, together with header information (variable names and domains). In this section, we apply operators to these basic factors, thus constructing an an expression in factor algebra.
In symfer this is accomplished using the central data type Factor. To be precise, an instance of (a subclass of) Factor represents a symbolic expression that will evaluate to a factor. For example, in the last three lines of
>>> from symfer import Multinom, SumProd
>>>
>>> weather = {'Weather':['sunny','rainy']}
>>> sprinkler = {'Sprinkler':['off','on']}
>>>
>>> weather_cpd = Multinom([weather],[0.8,0.2])
>>> sprinkler_cpd = Multinom([sprinkler, weather], [0.6,0.4,0.99,0.01] )
>>> joint = SumProd([], [weather_cpd, sprinkler_cpd])
we see three factors being defined; Multinom and SumProd are both Factor subclasses. The Multinom instances are “literal” atomic expressions, where the variables, domains and probabilities are explicitly specified. The SumProd instance is a composite expression, with two operands weather_cpd and sprinkler_cpd which are factor expressions themselves. The SumProd expression signifies that these operands should be multiplied, but the actual multiplication is not performed yet. In effect, as a Python object, a SumProd instance is little more than a container with pointers to the operands.
In parallel to the Python implementation, we also formalize the language of factor expressions in set theory. This formalization may clarify the meaning of the classes, and is also the source of equalities that justify replacing one factor expression with another. We call this formalization factor algebra.
Basic definitions¶
We assume a set of variables 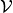 , a set of domains
, a set of domains 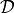 and a function
and a function
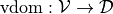 that assigns each variable a domain.
A
that assigns each variable a domain.
A 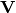 -assignment is a typed function that maps each variable
-assignment is a typed function that maps each variable 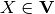 to a value
to a value 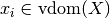 .
Here,
.
Here, 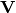 is a subset of
is a subset of 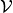 , and is called the assignment domain. An assignment
, and is called the assignment domain. An assignment  is
written using the syntax
is
written using the syntax 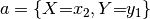 , which is shorthand for defining function
, which is shorthand for defining function  with
with
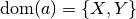 and values
and values 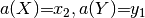 .
.
Now, a factor on 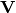 is a typed function from
is a typed function from 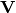 -assignments to numbers. For example,
factor
-assignments to numbers. For example,
factor 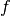 could map the assignment
could map the assignment 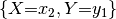 to the number
to the number 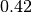 . This is also
written using a little shorthand:
. This is also
written using a little shorthand:
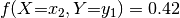
i.e. the set braces are omitted. With a little abuse of terminology, the assignment domain 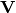 for
factor
for
factor 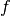 is also referred to as the factor’s domain, and written
is also referred to as the factor’s domain, and written 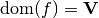 . However, keep
in mind that when we write this, we formally mean that
. However, keep
in mind that when we write this, we formally mean that 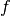 maps
maps 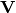 -assignments to numbers.
-assignments to numbers.
Note on implementation¶
Although we have just formally defined factors as functions in set theory, their implementation in symfer has little to do with what a computer scientist or software developer would consider a function. Factors are implemented as arrays, and it is often easier to think of them that way. The array appears when we list all possible assignments and corresponding function values:
| assignment | array of 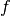 function values function values |
|---|---|
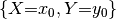 |
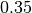 |
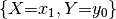 |
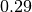 |
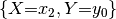 |
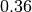 |
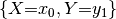 |
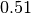 |
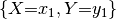 |
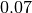 |
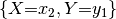 |
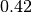 |
This is represented in symfer by storing:
- A Factor attribute domlist == ['X','Y'], listing the variables in
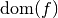 in a certain order
in a certain order - A Factor attribute domtypes, a dict containing
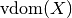 and
and 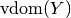 , for example
domtypes['X'] == ['x0','x1']
, for example
domtypes['X'] == ['x0','x1'] - The array of function values, in the above order (the first variable in domlist changes fastest in the assignment, and its values are enumerated in the order given by domtypes['X']). In Multinom factors, this array is listed in attribute par. In other Factor subclasses, the array is not stored at all, as the Factor merely represents a symbolic expression and not its result. Later, when the symbolic expression is evaluated (during the numeric phase), it is indeed constructed as a native array, which is faster than a Python list. The different evaluators, whose task this is, actually do use the same order.
Operators on factors¶
An operator we already came across in the introduction at the top of this page is factor multiplication.
The product of factor 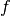 and factor
and factor 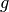 is written
is written 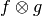 , and is itself a factor with domain
, and is itself a factor with domain 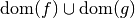 . Each of its values is
a product of an
. Each of its values is
a product of an 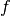 -value and a
-value and a 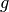 -value. For example, if
-value. For example, if 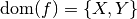 and
and
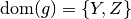 , then
, then 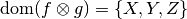 , and
, and
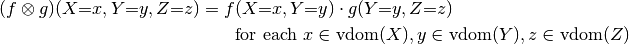
It is probably easier to get an idea of factor multiplication in terms of the arrays. Let’s assume that  is as shown in the table above, and the array of
is as shown in the table above, and the array of  is like this:
is like this:
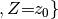 |
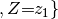 |
|
|---|---|---|
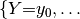 |
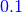 |
 |
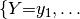 |
 |
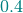 |
Then the array of 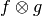 is like this:
is like this:
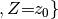 |
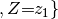 |
|
|---|---|---|
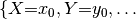 |
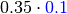 |
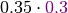 |
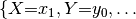 |
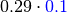 |
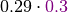 |
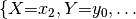 |
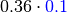 |
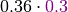 |
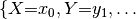 |
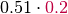 |
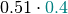 |
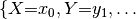 |
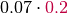 |
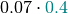 |
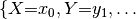 |
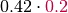 |
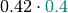 |
Note
The arrays are shown two-dimensionally here for legibility. If it were possible, we would have shown both the
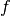 and
and 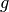 arrays two-dimensionally, and the
arrays two-dimensionally, and the 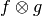 array three-dimensionally,
with each dimension matching one variable. As it is, the
array three-dimensionally,
with each dimension matching one variable. As it is, the 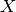 and
and 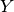 variables are collapsed into
one dimension.
variables are collapsed into
one dimension.
The second important operator is factor summation. This works a little different from normal summation; it
does not take two factor operands but only one (let’s say 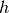 ). The other argument is a set of variables
). The other argument is a set of variables
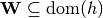 . These variables are summed out of the resulting factor. For example, if
. These variables are summed out of the resulting factor. For example, if
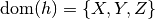 and we want to sum out
and we want to sum out 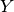 , we write
, we write 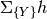 , or actually
, or actually
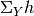 without the set braces because we are rather lazy than fussy. The resulting factor has
without the set braces because we are rather lazy than fussy. The resulting factor has
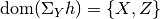 and values
and values
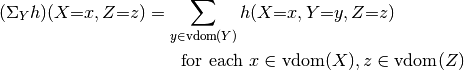
Continuing our example, with 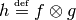 , the values of
, the values of 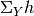 are:
are:
 |
 |
|
|---|---|---|
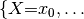 |
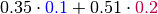 |
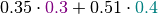 |
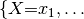 |
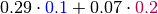 |
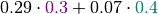 |
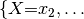 |
 |
 |
These are the most important operators in factor algebra; for the other, we refer to
Sander Evers, Peter J. F. Lucas: Marginalization without Summation: Exploiting Determinism in Factor Algebra. In: Weiru Lu (Ed.), Symbolic and Quantitative Approaches to Reasoning with Uncertainty - 11th European Conference, ECSQARU 2011, Proceedings, pp. 251-262 [SpringerLink] [preprint pdf]
Equalities¶
The definitions in factor algebra lead to some equalities, which are perhaps not very surprising, but useful to be aware of:
![f \prodjoin \I &= f\\
f \prodjoin g &= g \prodjoin f\\
f \prodjoin (g \prodjoin h) &= (f \prodjoin g) \prodjoin h\\
\sumproj_{V}\sumproj_{W} f &= \sumproj_{W}\sumproj_{V} f =\sumproj_{V,W}f\\
\sumproj_{V} \left( f \prodjoin g \right) &= \sumproj_{V} f \prodjoin g
\qquad\text{if $V {\in} \dom{f}, V {\notin} \dom{g}$}\\
\sumproj_{V} \left( f \prodjoin g \right) &= f \prodjoin \sumproj_{V} g
\qquad\text{if $V {\notin} \dom{f}, V {\in} \dom{g}$}\\
\bigl( \sumproj_{V} f \bigr)[W{=}d] &= \sumproj_{V} f[W{=}d]
\qquad\text{if $V{\neq}W, V{\notin}\dom{d}$}](_images/math/0a74730cd73175eaa26f0d364b2dfdd1b6293ed3.png)
Factor algebra to Factor¶
Operators in factor algebra correspond to subclasses of Factor. However, this correspondence is not completely one-to-one. The differences are:
- In a Factor, the order of the variables is defined. It is stored in the field domlist.
- Factor sum and product are merged into one operator SumProd. The reason for this is that this operator can be implemented efficiently; the summation is done in-place during the multiplication, so the operator does not require the memory to store the entire product.
- Operands of type Factor are always put in a list (even if there can be only one). This way an expression tree can be traversed in a uniform way. This list is always kept in a field fac.
- Similarly, deterministic factor operands (factors with integer values instead of probabilities) are kept in a field det.
A reason for this design is to keep a one-to-one correspondence with the YAML representation. To remove some
of the unpracticalities of directly working with this representation, convenience functions are introduced.
For example, instead of constructing 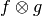 as symfer.SumProd([],[f,g]) one can also use
f.product(g). These convenience functions also behave smart in the sense that they take basic factor algebra
simplifications into account. For example, if either f or g is the identity factor I(), product
does not return a SumProd expression at all, but simply the other factor.
as symfer.SumProd([],[f,g]) one can also use
f.product(g). These convenience functions also behave smart in the sense that they take basic factor algebra
simplifications into account. For example, if either f or g is the identity factor I(), product
does not return a SumProd expression at all, but simply the other factor.
An overview of available factor algebra operators and their corresponding constructors and convenience functions is shown in the following table.
| factor algebra | Factor constructor | Factor convenience function |
|---|---|---|
|
SumProd(['A','B'],[f,g])
|
f.product(g).sumto(['A','B'])
or: I().product(f,g).sumto(...)
|
|
f = Multinom([{'A':[0,1]},..],
[0.25,0.75,..])
|
|
|
d = Fun([{'C':[False,True]}],
[{'A':[0,1],..],
[1,0,..])
|
|
|
Index([d],[h])
|
h.index(d)
|
|
Index([Fun([{'C':[False,True]}],
[],[1])],
[h])
|
h.index(C=True)
|
|
I()
|
|
|
Embed([d])
|
d.embed()
|
Reorder([{'newB':'B'},
{'newA':'A'}],
[f])
|
f.reorder([{'newB':'B'},
{'newA':'A'}])
|
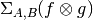
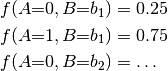
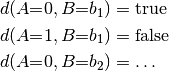
![h[C{=}d]](_images/math/b821c227c27efced285c1989a1cf7d1c2ade8a32.png)
![h[C{=}\text{true}]](_images/math/5987f6beb11ab25113dad80c5a4b2393e704db24.png)